Minterm ve Maxterm notasyonu
Σ (Toplam) ve Π (Çarpım) Notasyonu
Referans olması açısından bu bölüm bir Karnaugh haritasına atanan mintermleri ve maxtermleri tanımlamak için gerekli terminolojiyi ortaya koyar. Bunun dışında burada yeni bir şey yoktur.
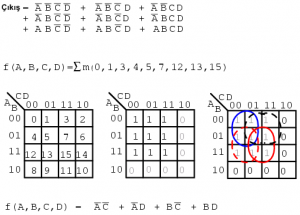
? (sigma) toplamı ve küçük harf “m” ise mintermleri ifade eder. ?m mintermlerin toplamını ifade eder. Sıradaki örnek bu noktayı açıklamak için verilmiştir. Sadeleştirilmemiş mantığı tanımlayan Boole denklemi yerine mintermleri listeleriz.
f(A,B,C,D) = ? m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15)
veya
f(A,B,C,D) = ?(m1,m2,m3,m4,m5,m7,m8,m9,m11,m12,m13,m15)
Numaralar aşağıda sağda gösterildiği gibi bir Karnaugh haritası içinde hücrelerin yerini veya adresini gösterir. Bu bir K-haritasında mintermlerin veya hücrelerin bir listesini tanımlamanın kısa bir yoludur.
Çarpımlar-ın-Toplamı çözümü bu yeni terminolojiden etkilenmez. Haritadaki mintermler, 1 ler daha önce olduğu gibi gruplandırılmıştır ve Çarpımlar-ın-Toplamı çözümleri yazılmıştır.
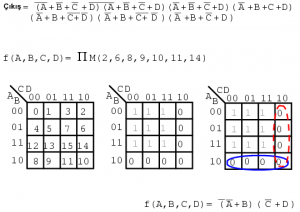
Aşağıda, maxtermlerden oluşan bir listeyi tanımlamak için gerekli terminolojiyi gösteriyoruz. Çarpım yunanca ? (pi) harfi ile gösterilir ve maxtermler büyük “M” harfi ile gösterilir. ?M maxtermlerin çarpımını gösterir. Aynı örnek bizim metodumuzu gösterir. Sadeleştirilmemiş mantığı tanımlayan Boole denklemi maxtermlerin bir listesiyle yer değiştirilmiştir.
f(A,B,C,D) = ? M(2, 6, 8, 9, 10, 11, 14)
veya
f(A,B,C,D) = ?(M2, M6, M8, M9, M10, M11, M14)
Numaralar K-haritasındaki hücrelerin adreslerinin yerlerini belirtir. Aşağıda gösterildiği gibi maxtermler için bu 0 ların olduğu yerdir. Toplamlar-ın-Çarpımı çözümü bilindik şekilde tamamlanmıştır.

Son yorumlar