Karnaugh Haritaları ile Mantık Sadeleştirme
Şimdiye kadar yaptığımız mantık sadeleştirme örnekleri Boole cebri ile aynı hızda yapılabilirdi. Gerçek dünyada mantık sadeleştirme problemleri daha büyük Karnaugh haritaları gerektirir ve çok fazla iş yapmak gerekir. Bu bölümde bazı suni örnekler yapacağız gerçek dünya uygulamalarının çoğunu Tümleşik Mantık bölümüne bırakacağız. Suni örnek ile teknikleri gösteren örnekler kastedilmiştir. Bu yaklaşım bize Tümleşik Mantık bölümünde daha kompleks uygulamalara geçişte gerekli olan donanımı kazandıracaktır.
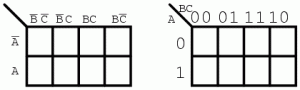
Daha önce geliştirdiğimiz Karnaugh haritasını gösterelim.
Haritanın üstündeki sayıların dizisine dikkat edin. 00, 01, 10, 11 gibi olması gereken ikili sayı dizisi değil. Sayı dizisi 00, 01, 11 10 bu dizi Gray kodu dizisidir. Gray kodu dizisinde ikili sistemin aksine, bir sayıdan diğerine geçerken bir ikili bit değişir. Bunun anlamı komşu hücreler sadece bir bit veya bir Boole değişkeni değiştirir. Bir mantık fonksiyonunun çıkışlarının ortak noktalarını görebileceğimiz şekilde organize etmek için gereken şey budur. Ayrıca, sütun ve satır başlıkları Gray kodu şeklinde olmalıdır aksi halde harita bir Karnaugh haritası olmaz. Ortak Boole değişkenlerini paylaşan hücreler komşu olmaz ve görsel düzen göstermez. Komşu hücreler sadece bir bit değişir çünkü bir Gray kodu dizisi de sadece bir bit değişir.
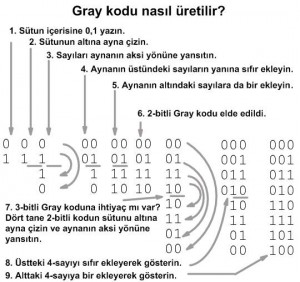
Eğer kendi Karnaugh haritalarımızı çizersek, kullandığımız harita büyüklüğü için Gray kodu üretmemiz gerekir.Bu şekilde her büyüklük için Gray kodu üretiriz.
Yukarı sağdaki Gray kodu dizisi listede yukarıdan aşağıya veya aşağıdan yukarıya gittikçe bir bit değiştiğine dikkat edin. Gray kodunun bu özelliği genelde sayısal elektronikte çok kullanışlıdır. Özellikle Karnaugh haritalarına uygulanabilir.
Şimdi 3-değişkenli Karnaugh haritalarının sadeleştirilmesine geçelim. Sadeleştirilmemiş mantığın çarpım terimlerinin K-haritasına nasıl eşleştirildiğine bakalım. Sayısal mantığın çarpımların toplamı sadeleştirmesine götüren komşu hücre gruplarının nasıl tanımlandığına bakalım.
Yukarıda herbir çarpım terimi için 1’leri yerleştiriyoruz, ikili bir grubu belirliyoruz, sonra sadeleştirilmiş sonuç olarak grubun tamamı için tek bir çarpım terimi yazıyoruz.
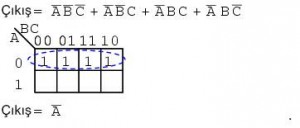
Yukarıda dört çarpım terimini eşleştirmek, A’ Boole terimi ile kapsanan dörtlü bir grup oluşturur.
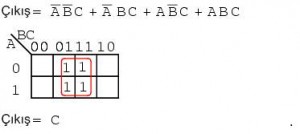
Dört çarpım terimini eşleştirmek, bir değişkenli C tarafından kapsanan dörtlü bir grup oluşturur.
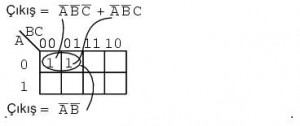
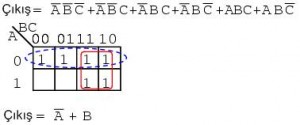
Yukarıda altı çarpım terimini eşleştirdikten sonra, yukarıdaki dörtlü grubu tanımlayın, alttaki iki hücreyi dörtlü bir grup gibi iki hücreyi diğer bir grupla paylaşarak seçin. Bu ikisini dörtlü bir grupla kapsamak daha kolay sonuç verir. İki grup olduğu için,A’+B çarpımların toplamı sonucunda iki çarpım terimi olacaktır.
Yukarıdaki iki çarpım terimi ikili bir grup oluşturur ve BC ye sadeleşir.
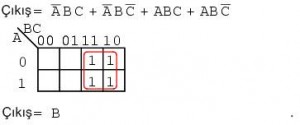
Dört çarpım terimini eşleştirmek dörtlü bir grup oluşturur ve bu grup B dir.
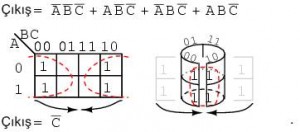
Yukarıda dört çarpım terimini eşleştirmek dörtlü bir grup oluşturur. Dörtlü grubu, haritanın uçlarını bir silindir oluşturacak şekilde yuvarlayarak ve sonuçta hücreleri komşu yaparak görebiliriz. Normalde dörtlü grubu yukarıda soldaki gibi belirtiriz. A, B, C değişkenleri dışında ortak bir C’ değişkeni de vardır. C’ bütün dört hücre için 0 dır. Nihai sonuç C’ dür.
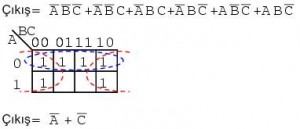
Yukarıda, sadeleştirilmemiş denklemin altı hücresi dörtlü iki grup halinde düzenlenebilir. Bu iki grup bize A’ + C’ nün sadeleştirilmiş sonucunda iki çarpım terimi vermelidir.
Aşağıda, Boole cebri bölümünden Zehirli Atık Yakma Fırınını tekrar görüyoruz. Bu örneğin detayları için Boole cebri bölümüne bakınız. Mantığı bir Karnaugh haritası kullanarak sadeleştireceğiz.
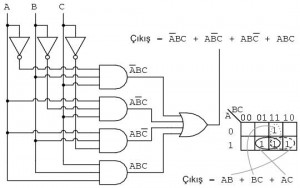
Çıktı olan Boolean denklemi dört çarpım terimine sahiptir. Dört 1’i karşılık gelen çarpım terimleri ile eşleştirin. Hücre gruplarını oluşturarak, ikili üç grup elde ederiz. Her bir grup için bir adet çarpım terimi olmak üzere sadeleştirilmiş sonuçta toplam üç çarpım terimi olacaktır. Aşağıda gösterilen sonucun kapı diyagramı için, Boole cebri bölümünden “Zehirli Atık Yakma Fırını” konusuna bakınız.
Aşağıda, karşılaştırma yapmak için Zehirli Atık Yakma Fırınının Boole cebri ile sadeleştirilmesini tekrar ediyoruz.
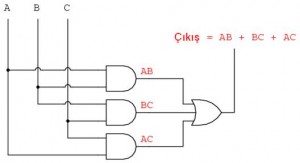
Aşağıda, yukarıdaki Boole cebri ile yapılan sadeleştirme ile karşılaştırma yapmak için Zehirli Atık Yakma Fırınının Karnaugh haritası çözümünü tekrar ediyoruz. Bu durum Karnaugh haritasının mantık sadeleştirme için neden çokça kullanıldığını gösteriyor.
Karnaugh haritası metodu, önceki sayfadaki Boole cebrinden daha kolay gözükmektedir.
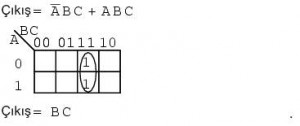



Sayın hocam: inanın çok ama çoook acemiyim hiç bir temelim yok bu konuda. Aşağıdaki yazdığım fonksiyonların ikilik sistemde karşılıkları, karnaugh haritası ve indirgeme sonucu ile devre şekli çizimi konulu bir soru ile karşı karşıyayım. Nasıl çözüleceğine dair benim gibi birisinin anlayacağı şekilde anlatıp yada çözümünü verebilirmisiniz. İnanın mintertar olurum.
F=Ʃ 0,1,6,7,8,9,14,15
F=π 2,3,4,5,10,11,12,13
Merhabalar hocam. Ben karnaugh haritalarini kolaylikla cizebiliyorum fakat son kisma gelince tikaniyorum. Son kisimdaki sadelestirme islemini daha acik bir sekilde anlatabilirmisiniz? Tesekkur ederim. Iyi calismalar.
Merhaba Gurkan , zamanım olursa video çekerek örnekler yapacağım .
Sayın Hocam öğretmenim bana ödev verdi bana karno haritasının (2,3,4 değişkenli örneklerle açıklayınız) dedi ben bu ödevi nasıl yapa bilirim lütfen yardım edin
Merhaba Emre , eğer bu yazıyı iyi anladıysan gayet basit bir şekilde ödevini yapabileceğine inanıyorum , kolay gelsin.